a) Optimal application of de-aliasing models

In order to investigate the impact of temporal aliasing errors in more detail, tidal and non-tidal aliasing errors were assessed individually, by excluding either the one or the other error signal from the simulation, but keeping the same product-error assumptions for all simulations. Results demonstrate that the orbit altitude is the main performance driver, either omitting ocean tide errors or omitting errors due to non-tidal aliasing. If non-tidal AO signals are included in the simulation, lower orbit altitudes lead to significantly reduced temporal aliasing errors, even in the longer wavelength spectrum, as temporal aliasing errors due to AO error is the dominating error contributor. In this context, it is to mention that the altitude of the inclined pair is crucial since an altitude, which is much lower (e.g. below 400 km) than the one of the polar pair, results into smaller retrieval errors, also in the high frequency spectrum. If no AO signals are included in the simulation and tidal aliasing errors are dominating, the performances of gravity field solutions of double pair formations having different altitudes show similar behavior at the low-to-mid degree spectrum. In that case, the role of orbit altitude becomes more important for the performance at the mid-to-high frequency spectrum. For sub-monthly retrievals, the length of the respective retrieval period plays an important role as well, next to the altitude. This is especially true if non-tidal AO signals are included. 

b) Treatment of ocean tides in NRT analysis and post-processing

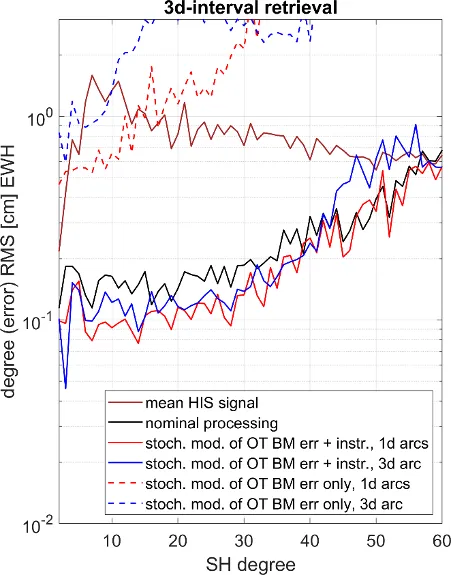
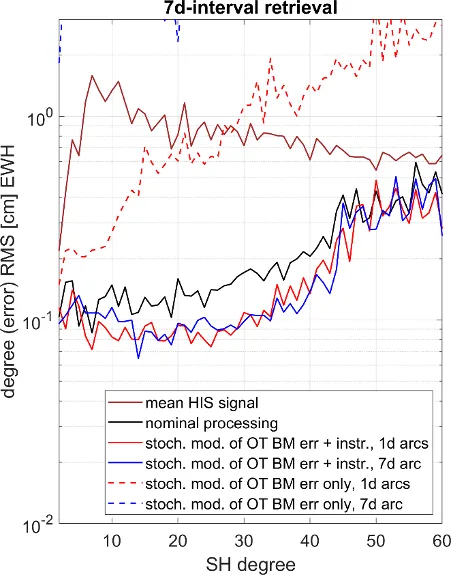
It could be shown by Hauk and Pail (2018) that the co-estimation of ocean tide parameters is possible and reduces temporal aliasing errors. However, this method requires long observation time series and is therefore not applicable in near-real time (NRT) analysis. Therefore, an alternative method was developed and applied to Bender double-pair constellations. It is based on the idea to introduce ocean tide background model errors as additional stochastic model into the parameter adjustment, and to propagate it through the whole process to the parameter estimates. Details of the method and a detailed analysis for single- and double pair scenarios can be found in Abrykosov et al. (2021). 

The results of Figures 1, which are based on a 3d_H Bender-type double-pair scenario, demonstrate that stochastic modelling of OT background errors has the potential to significantly improve the retrieval performance. This method can be applied not only to the retrieval of long-term, e.g. monthly, solutions, but also short-interval fields. It thus poses a valid processing strategy for estimating NRT-type gravity field solutions. The main limiting factor are non-tidal (AOD) background model errors. In future research, it is planned to develop a similar strategy for stochastic modelling of non-tidal background model errors, and apply it together with the OT method discussed here.

c) Optimal signal parametrization with respect to space and time

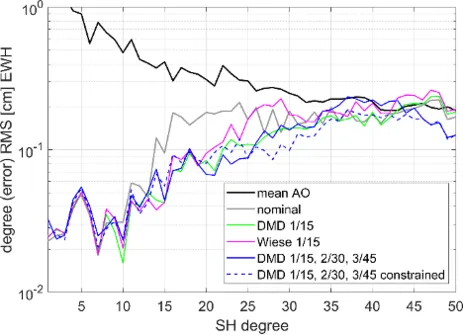
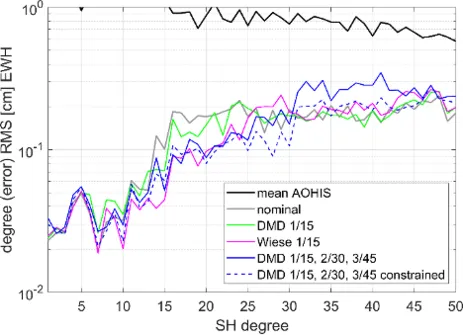
An alternative method for the co-estimation of daily long-wavelength gravity fields together with coefficients of higher SH degrees (“Wiese approach”), the data-driven multistep self-de-aliasing (DMD) method, has been developed (Abrykosov et al. 2022a), originally for the “self-de-aliasing” of the single-pair missions GRACE and GRACE-FO. In the course of this, a detailed analysis of the space-time pattern of temporal gravity signals was performed, showing that also long-term signals create high-frequency spatial structures. Therefore, the standard concept proposed by Wiese et al. (2011) is not able to fully capture these signals. It was demonstrated that especially in this case of a single-pair scenario  long-wavelength, high-amplitude signal components are mapped into other spectral bands, thus degrading the retrieval performance. Therefore, the decoupling of daily low-degree and multi-daily higher-degree estimates, as done in DMD, is of great benefit especially for single-pair scenarios, because the effect of aliasing reduction by means of daily estimates is larger than the spectral leakage due to decoupling of low and higher degrees. 

In the frame of this project, the DMD concept was transferred to double-pair constellations. Here, compared to single-pair constellations the behavior of DMD is somewhat different, because of the intrinsic aliasing reduction of the double-pair constellation due to the additional inclined pair, leading to a lower gain of additional de-aliasing relative to the spectral leakage effect. The DMD performance depends on the amplitude of the signal (being a potential source of aliasing) and the resolution of the gravity field product (defining the relative contribution of spectral leakage errors). Figures 2a and 2b show the results when using only AO or the full AOHIS signal as an input, respectively. Evidently, the classical Wiese parametrization performs slightly better for the present simulation set-up, including the full AOHIS signal up to degree/order 50. However, both classical Wiese and DMD perform generally better than the nominal processing without additional parametrization. 

In addition, expanding the classic “Wiese approach” with additional intermediate steps in terms of successively longer periods increases the processing complexity, but has not shown any improvements in achievable gravity performance. In contrast, as shown in Figure 10, a DMD multi-step approach has some potential to further improve the results.

d) Analysis of need for long-term trend estimation

Linear trend parameters have been co-estimated together with monthly temporal gravity fields for a 10-year period in the frame of a joint adjustment. Comparing the monthly solutions with and without co-estimation, there is no indication of a benefit when the long-term trend is co-estimated.

e) Analysis of need for post-processing

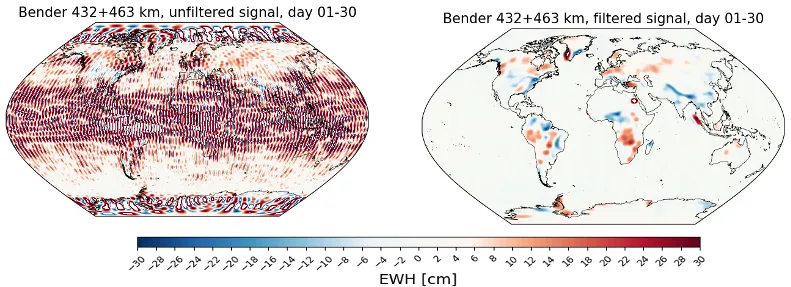
An optimal filter technique for post-processing of Bender-type gravity field solutions was developed. Methods based on non-isotropic smoothing by approximate decorrelation and regularization (DDK), and time variable decorrelation (VADER/VDK filters) were investigated. The VDK filter usually outperforms the DDK filter. Exemplarily, Figure 3 shows the results of a raw and a VDK-filtered solution of the Bender-pair scenario 3d_H. Comparing single and double-pair solutions, a much lower filter strength has to be applied to reduce the residual striping of double-pair missions.